[변리사 2차-1번] 구간 히프 (Interval Heap)

 

2019년 제 56회 변리사 2차 데이터 구조론 2교시 1번 문제 해설

 

 

1. 구간히프를 정의하고, 그 특성에 관하여 설명하시오.(5점)

 

* 먼저 heap이란?

 

숫자의 최대값, 최소값을 빠르게 탐색하기 위해 고안된 완전이진트리 (Complete Binary Tree)이다. 기본적인 Heap의 각 노드는 하나의 숫자로 이루어져 있으며 삽입,삭제시 리프노드부터 시작하여 부모-자식간의 대소판별 경쟁을 통해 최소 또는 최대값이 항상 루트 노트들 차지한다. 이러한 성질 때문에 우선순위큐 (Priority Queue)는 최소,최대 힙으로 만들어져있다.

 

 

* 구간 Heap?

 

구간 히프는 Heap과 동일한 완전이진트리의 형태면서 각각의 노드는 최대 두개의 숫자로 구성 되어있다.

노드에 적힌 두개의 숫자는 폐구간 [a,b]이고 자식과 부모의 구간 관계는 세그먼트트리(Segment Tree)처럼 자식들의 구간은 부모 구간에 포함된다. 즉, 위 그림에서 최상위 루트 노드 [2,30]의 모든 자식들은 폐구간 [2,30]안에 포함된다는 뜻이다. 각 노드에서의 폐구간 [a,b]에서 왼쪽 a값은 최소값, b는 최대값을 뜻하며 이것은 사실 최소힙과 최대힙을 동시에 합쳐 표현한 완전이진트리형태라고 볼 수 있다.

 

 

 

즉, 최소,최대 힙이 합쳐진 형태의 트리로서 양 쪽 끝 우선순위 큐(DEPQ : Double-ended priority queue) 라는 자료구조로 쓰이며 네트워크 버퍼나 외부 퀵정렬에 활용된다.

 

 

2. 다음 과 같은 구간히프에 의해 정의된 최소히프와 최대히프를 각각 그리시오. (10점)

 

 

 

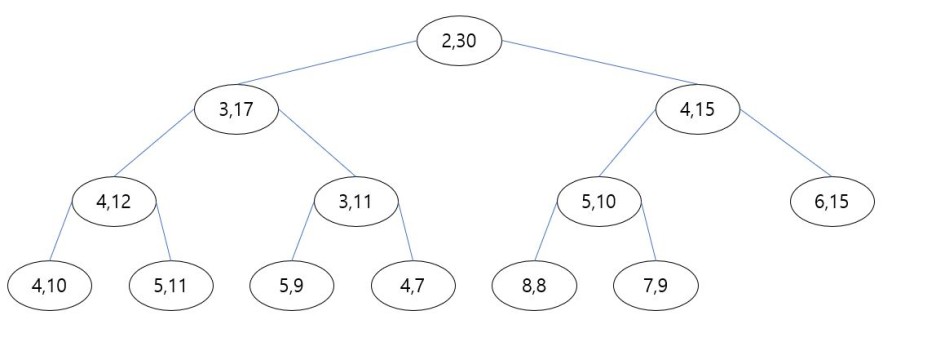
1번 문제의 해설에서 언급한 바와 같이 각 노드의 폐구간 [a,b]에서의 a값은 최소힙, b값은 최대힙에서의 값이라고 보면 된다. 즉, 각 노드의 a로만 이루어진 트리와 b로만 이루어진 트리로 분리시키면 최소힙, 최대힙이 된다.

 

 

 

3. 문제 (2)의 구간히프에 40과 32를 차례대로 삽입할 때 각각의 구간히프를 그리시오. (10점)

 

 

Step 1. 40을 가장 끝 빈 리프노드 자리에 삽입

 

 

 

 

Step 2. 부모 노드의 최대힙 값 ([6,15]에서 15)보다 크므로 자리 Swap

 

 

 

 

Step 3. 새로운 부모노드인 [4,15]와 비교, 15보다 크므로 자리 Swap

 

 

 

 

Step 4. 새로운 부모노드인 [2,30]과 비교, 30보다 크므로 자리 Swap. 루트까지 확인했으므로 종료.

 

 

Step 5. 같은 방식으로 32을 삽입한 후 결과

 

 

 

 

 

4. 문제 (3)에서 마지막으로 만들어지는 구간히프에서 최소 원소를 제거한 후의 구간히프를 그리시오. (10점)

 

Step 1. 가장 최소원소 제거를 위해 루트 노드의 [2,40]에서 왼쪽값 (최소힙)을 제거한다. 이때, 가장 마지막 노드의 최소 값(왼쪽 값)에 해당하는 15와 비교하면서 루트부터 확인하며 자리를 찾아간다.

 

 

 

 

 

Step 2. 루트의 첫번째 좌측 자식의 최소힙 값 ([3,17]에서 3) 과 P값 비교, P값보다 작으므로 Swap

 

 

 

 

 

Step 3. Swap된 결과 노드인 [15,17] (=[P,17])의 자식 노드의 최소값 4(왼쪽 자식), 3(오른쪽 자식) 중 3이 더 작으므로 우측 자식의 최소힙 값 3과 Swap.

스왑 된 우측 자식 노드는 [15,11]의 형태가 되는데 폐구간 트리 형태를 유지하기 위해서 15와 11또한 Swap. 이때 최소값 비교 기준이던 P값인 15 또한 11로 Update

 

 

 

 

 

Step 4. 동일한 방법으로 마지막 최종 리프 노드와 비교후 Step 3와 동일한 이유로 최종 노드 폐구간 결정 후 종료

 

 

 

 

 

 

 

 

+ 학원에도 포스팅 : https://blog.naver.com/mario002/221978255957

 

 

 

 

* 참고 자료 

https://en.wikipedia.org/wiki/Double-ended_priority_queue

Double-ended priority queue - Wikipedia