[56회 변리사 2차-2번] 최소신장트리(MST)

 

2019년 제 56회 변리사 2차 데이터 구조론 2교시 2번 문제 해설

 

 

 

MST (Minimum Spanning Tree)

 

그래프 G에서 모든 정점을 연결하여 갈수 있도록 하되, 

최소의 간선개수와 최소의 가중치로 이루어진 트리를 말한다.

(즉, 정점 개수 V , 간선 개수 V-1, 간선은 무방향)

 

 

1. 그래프 G에 관하여 다음 물음에 답하시오

 

 

 

=> 정점(Vertax) 의 개수 8

=> 따라서 MST를 만족하는 간선의 개수 (8-1) = 7 개를 선택하면 된다.

=> 이 그래프에서의 MST가 가지는총 가중치의 합은 10이다.

 

=> 즉, 가중치의 합이 10인 MST를 구하는 3가지 알고리즘을 해설 한다.

 

 

 

(1) 그래프 G에 대해 프림 알고리즘 (Prim's Algorithm)으로 최소신장트리를 구하는 과정을 나타내시오. (단, 노드 A를 시작 정점으로 선택한다.) (7점)

 

*Prim's Algorithm

탐욕 기법(Greedy)처럼 특정 정점에서 시작하여, 정점에 인접한 간선들 중 가장 가중치 (cost)값이 낮은 간선만을 선택하는 알고리즘이다. 코드로 구현시 보통 우선순위큐와 방문처리를 통해 다익스트라와 흡사하게 구현한다.

 

Step 1. 정점 A에서 인접한 정점 가중치 정보 2,1,6의 간선들 중 가장 가중치가 낮은 1 (A,B)을 선택.

가중치 정보 : 2,6

 

 

 

 

 

 

 

Step 2.정점 B에서 인접한 정점 가중치 정보 2,1,4 추가

알고있는 가중치 정보 : 2,6,2,1,4 중 가장 작은 1 (B-C) 선택

가중치 정보 : 2,6,2,4

 

 

 

 

 

 

 

Step 3.정점 C에서 인접한 정점 가중치 정보 4 추가

알고있는 가중치 정보 : 2,6,2,4,4 중 가장 작은 2 중에서 임의의 간선 선택

(A-F) ,(B-D) 중 (B-D) 선택

가중치 정보 : 2,6,4,4

 

 

 

 

 

 

Step 4. 정점 D에서 인접한 정점 가중치 정보 1,2 추가

알고있는 가중치 정보 : 2,6,4,4,1,2 중 가장 작은 1 선택 (D-F)

가중치 정보 : 2,6,4,4,2

 

 

 

 

 

 

Step 5.정점 F에서 인접한 정점 가중치 정보 2,2 추가

알고있는 가중치 정보 : 2,6,4,4,2,2,2 중 2에 해당하는 가중치에서 아직 방문하지 못한 정점을 잇는 (F-E),(F-H) 중 임의의 간선 (F-E) 선택

가중치 정보 : 2,6,4,4,2,2

 

 

 

 

 

 

 

 

 

Step 6.정점 E에서 인접한 정점 가중치 정보 추가

알고있는 가중치 정보 : 2,6,4,4,2,2,4,1... 중 가중치가 가장 낮은 1 (E-G) 선택

가중치 정보 : 2,6,4,4,2,2,4,2.....

 

 

 

 

 

 

Step 7.마지막으로 아직 방문하지 못한 H에 대해서

가중치 정보중에서 가장 낮은 가중치인 2를 가지면서 H로 가는 간선

(F-H)를 선택 후 종료

 

 

 

 

 

 

 

(2) 그래프 G에 대해 크루스칼 알고리즘(Kruskal's Algorithm)으로 최소신장트리를 구하는 과정을 나타내시오. (단, 간선 A-B를 먼저 선택한다.) (7점)

 

*Kruskal's Algorithm

탐욕 기법(Greedy)처럼 특정 간선에서 시작하여 가중치가 낮은 간선만 골라서 이어 붙이는 방식이다. 모든 간선중 가장 낮은 간선부터 선택하면서 붙여나가 사이클 없이 (V(정점개수) -1 개)를 결정하면 완성된다. 가중치가 같을 땐 임의의 간선을 선택하되, 사이클이 생기지 않는 간선을 선택한다.

코드로 구현시 보통 간선리스트를 가중치 기준으로 오름차순 정렬 후, 유니온 파인드로 구현한다.

 

 

Step 1.문제 조건에 의해 간선 A-B를 선택

 

 

 

 

 

 

Step 2.아직 선택되지 않은 간선 중 가장 가중치가 낮은 임의의 간선에서

B-C (가중치 : 1)를 선택

 

 

 

 

 

 

 

Step 3.아직 선택되지 않은 간선 중 가장 가중치가 낮은 임의의 간선에서

F-D (가중치 : 1)를 선택

 

 

 

 

 

 

Step 4.아직 선택되지 않은 간선 중 가장 가중치가 낮은 임의의 간선에서

E-G (가중치 : 1)를 선택

 

 

 

 

Step 5.아직 선택되지 않은 간선 중 가장 가중치가 낮은 임의의 간선에서 사이클이 생기지 않는 A-F(가중치 2) 선택

 

 

 

 

 

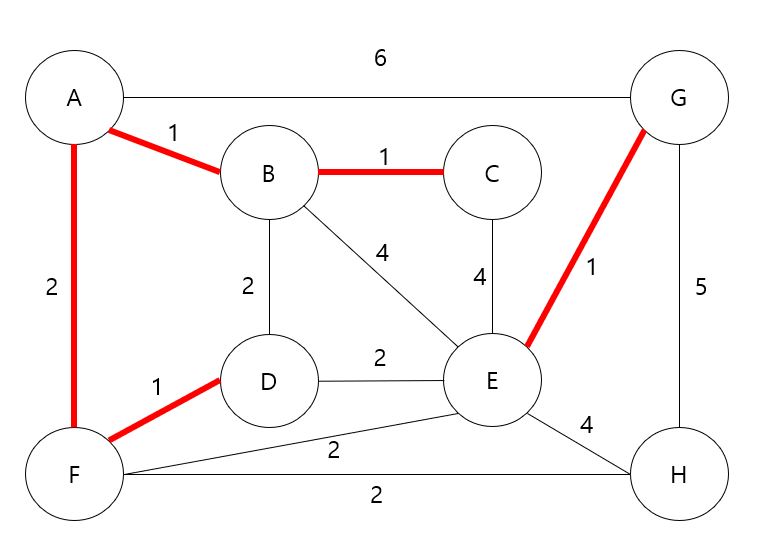
Step 6.아직 선택되지 않은 간선 중 가장 가중치가 낮은 임의의 간선에서 사이클이 생기지 않는 F-E(가중치 2) 선택

 

 

 

 

 

 

Step 7.아직 선택되지 않은 간선 중 가장 가중치가 낮은 임의의 간선에서 사이클이 생기지 않는 F-H(가중치 2) 선택 후 끝

 

 

 

 

 

 

 

(3) 그래프 G에 대해 솔린 알고리즘(Sollin's Algorithm)으로 최소신장트리를 구하는 과정을 나타내시오. (단, 간선 A-B를 먼저 선택한다.) (6점)

 

*Sollin's Algorithm

탐욕 기법(Greedy)처럼 최소의 간선만을 선택해 나간다. Sollin's Algorithm 같은 경우는 한 스텝에 여러개의 간선을 선택한다. 각 정점을 하나씩 확인하면서 정점의 간선들 중 최소의 가중치만 선택하고 중복 선택을 허용한다. 한 스텝이 끝나면 간선의 선택으로 인해 정점의 집합들(Forest)이 생기는데 이러한 집합과 집합을 잇는 간선들 중 마찬가지로 최소의 간선을 선택하여 집합과 집합을 합쳐나가다가 MST를 형성하는 순간 종료한다.

 

 

Step 1.모든 정점을 하나씩 확인하면서 각 정점에 달린 간선 중 최소 가중치 간선만 전부 선택한다.

 

정점 A의 인접 정점 중 가중치 1이 가장 작으니 A-B 선택

정점 B의 인접 정점 중 가중치 1이 가장 작으니 B-A 선택 (중복 선택 허용)

정점 C의 인접 정점 중 가중치 1이 가장 작으니 C-B 선택

정점 D의 인접 정점 중 가중치 1이 가장 작으니 D-F 선택

정점 E의 인접 정점 중 가중치 1이 가장 작으니 E-F 선택

정점 F의 인접 정점 중 가중치 1이 가장 작으니 F-D 선택 (중복 선택 허용)

정점 G의 인접 정점 중 가중치 1이 가장 작으니 G-E 선택(중복 선택 허용)

정점 H의 인접 정점 중 가중치 2가 가장 작으니 H-F 선택

 

 

 

 

 

 

 

 

 

 

 

Step 2.형성된 1~3개의 집합(Forest)에서 집합과 집합을 잇는 간선들 중 최소의 간선을 선택한다.

 

1번 집합에서 2번 집합, 3번 집합을 잇는 간선들 중 가장 작은 간선은

가중치 2를 가진 (A-F) 와 (B-D) 이다. 둘 중 임의의 간선을 선택한다.

여기서는 A-F 를 선택.

 

2번 집합에서 1번 집합, 3번 집합을 잇는 간선들 중 가장 작은 간선은

가중치 2를 가진 (E-D) 이다.

 

3번 집합에서 1번 집합, 2번 집합을 잇는 간선들 중 가장 작은 간선은

가중치 2를 가진 간선들인데 이미 1번 집합과 2번집합에서 연결을 결정 했으므로

결정된 (F-A)와 (D-E)를 선택.

 

여태까지 연결한 간선의 개수가 7개이며 8개의 정점으로 하나의 집합이 형성되었고 가중치 합산 값이 10이므로 MST 조건에 충족한다.